Semidefinite programming
From Wikipedia, the free encyclopedia
Semidefinite programming (SDP) is a subfield of convex optimization concerned with the optimization of a linear objective function over the intersection of the cone of positive semidefinite matrices with an affine space, i.e., a spectrahedron.Semidefinite programming is a relatively new field of optimization which is of growing interest for several reasons. Many practical problems in operations research and combinatorial optimization can be modeled or approximated as semidefinite programming problems. In automatic control theory, SDP's are used in the context of linear matrix inequalities. SDPs are in fact a special case of cone programming and can be efficiently solved by interior point methods. All linear programs can be expressed as SDPs, and via hierarchies of SDPs the solutions of polynomial optimization problems can be approximated. Finally, semidefinite programming has been used in the optimization of complex systems.
Contents |
Motivation and definition
Initial motivation
A linear programming problem is one in which we wish to maximize or minimize a linear objective function of real variables over a polyhedron. In semidefinite programming, we instead use real-valued vectors and are allowed to take the dot product of vectors. Specifically, a general semidefinite programming problem can be defined as any mathematical programming problem of the formEquivalent formulations
An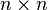 matrix
matrix 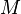 is said to be positive semidefinite if it is the gramian matrix of some vectors (ie. if there exist vectors
is said to be positive semidefinite if it is the gramian matrix of some vectors (ie. if there exist vectors  such that
such that  for all
for all  ). If this is the case, we denote this as
). If this is the case, we denote this as  . Note that there are several other equivalent definitions of being positive semidefinite.
. Note that there are several other equivalent definitions of being positive semidefinite.Denote by
 the space of all real symmetric matrices. The space is equipped with the inner product (where
the space of all real symmetric matrices. The space is equipped with the inner product (where  denotes the trace)
denotes the trace) 
We can rewrite the mathematical program given in the previous section equivalently as
 in
in  is given by
is given by  from the previous section and
from the previous section and  is an
is an 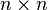 matrix having
matrix having  th entry
th entry  from the previous section.
from the previous section.Note that if we add slack variables appropriately, this SDP can be converted to one of the form
 as a diagonal entry (
as a diagonal entry ( for some
for some 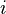 ). To ensure that
). To ensure that  , constraints
, constraints  can be added for all
can be added for all  . As another example, note that for any positive semidefinite matrix
. As another example, note that for any positive semidefinite matrix  , there exists a set of vectors
, there exists a set of vectors 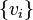 such that the
such that the 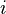 ,
, 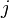 entry of
entry of  is
is  the scalar product of
the scalar product of 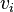 and
and  .
Therefore, SDPs are often formulated in terms of linear expressions on
scalar products of vectors. Given the solution to the SDP in the
standard form, the vectors
.
Therefore, SDPs are often formulated in terms of linear expressions on
scalar products of vectors. Given the solution to the SDP in the
standard form, the vectors 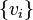 can be recovered in
can be recovered in 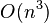 time (e.g., by using an incomplete Cholesky decomposition of X).
time (e.g., by using an incomplete Cholesky decomposition of X).Duality theory
Definitions
Analogously to linear programming, given a general SDP of the form and
and  ,
,  means
means  .
.Weak duality
The weak duality theorem states that the value of the primal SDP is at least the value of the dual SDP. Therefore, any feasible solution to the dual SDP lower-bounds the primal SDP value, and conversely, any feasible solution to the primal SDP upper-bounds the dual SDP value. This is becauseStrong duality
Under a condition known as Slater's condition, the value of the primal and dual SDPs are equal. This is known as strong duality. Unlike for linear programs, however, not every SDP satisfies strong duality; in general, the value of the dual SDP may lie strictly below the value of the primal.(i) Suppose the primal problem (P-SDP) is bounded below and strictly feasible (i.e., there exists
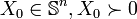 such that
such that  ,
,  ). Then there is an optimal solution
). Then there is an optimal solution  to (D-SDP) and
to (D-SDP) and for some
for some  ). Then there is an optimal solution
). Then there is an optimal solution  to (P-SDP) and the equality from (i) holds.
to (P-SDP) and the equality from (i) holds.Examples
Example 1
Consider three random variables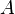 ,
, 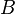 , and
, and  . By definition, their correlation coefficients
. By definition, their correlation coefficients 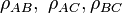 are valid if and only if
are valid if and only if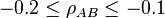 and
and  . The problem of determining the smallest and largest values that
. The problem of determining the smallest and largest values that  can take is given by:
can take is given by:- minimize/maximize

- subject to



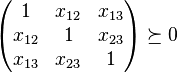
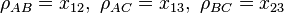 to obtain the answer. This can be formulated by an SDP. We handle the
inequality constraints by augmenting the variable matrix and introducing
slack variables, for example
to obtain the answer. This can be formulated by an SDP. We handle the
inequality constraints by augmenting the variable matrix and introducing
slack variables, for example
Solving this SDP gives the minimum and maximum values of
 as
as  and
and  respectively.
respectively.Example 2
Consider the problem- minimize

- subject to
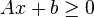
 whenever
whenever 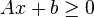 .
.Introducing an auxiliary variable
 the problem can be reformulated:
the problem can be reformulated:- minimize

- subject to

 .
.The first restriction can be written as
 is the square matrix with values in the diagonal equal to the elements of the vector
is the square matrix with values in the diagonal equal to the elements of the vector  .
.The second restriction can be written as
- det
![\underbrace{\left[\begin{array}{cc}t&c^Tx\\c^Tx&d^Tx\end{array}\right]}_{D}\geq 0](http://upload.wikimedia.org/wikipedia/en/math/4/7/1/4716c3a1c00adcf62801a21e76330fdb.png)
 .
.The semidefinite program associated with this problem is
- minimize

- subject to
![\left[\begin{array}{ccc}\textbf{diag}(Ax+b)&0&0\\0&t&c^Tx\\0&c^Tx&d^Tx\end{array}\right] \succeq 0](http://upload.wikimedia.org/wikipedia/en/math/a/7/3/a73fe310dadd0470b5e627217fa60e1a.png)
Example 3 (Goemans-Williamson MAX CUT approximation algorithm)
Semidefinite programs are important tools for developing approximation algorithms for NP-hard maximization problems. The first approximation algorithm based on an SDP is due to Goemans and Williamson (JACM, 1995). They studied the MAX CUT problem: Given a graph G = (V, E), output a partition of the vertices V so as to maximize the number of edges crossing from one side to the other. This problem can be expressed as an integer quadratic program:- Maximize
 such that each
such that each  .
.
- Relax the integer quadratic program into an SDP.
- Solve the SDP (to within an arbitrarily small additive error
 ).
). - Round the SDP solution to obtain an approximate solution to the original integer quadratic program.
 such that
such that  , where the maximization is over vectors
, where the maximization is over vectors 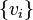 instead of integer scalars.
instead of integer scalars.
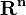 ;
since the vectors are not required to be collinear, the value of this
relaxed program can only be higher than the value of the original
quadratic integer program. Finally, a rounding procedure is needed to
obtain a partition. Goemans and Williamson simply choose a uniformly
random hyperplane through the origin and divide the vertices according
to which side of the hyperplane the corresponding vectors lie.
Straightforward analysis shows that this procedure achieves an expected approximation ratio
(performance guarantee) of 0.87856 - ε. (The expected value of the cut
is the sum over edges of the probability that the edge is cut, which is
proportional to the angle
;
since the vectors are not required to be collinear, the value of this
relaxed program can only be higher than the value of the original
quadratic integer program. Finally, a rounding procedure is needed to
obtain a partition. Goemans and Williamson simply choose a uniformly
random hyperplane through the origin and divide the vertices according
to which side of the hyperplane the corresponding vectors lie.
Straightforward analysis shows that this procedure achieves an expected approximation ratio
(performance guarantee) of 0.87856 - ε. (The expected value of the cut
is the sum over edges of the probability that the edge is cut, which is
proportional to the angle  between the vectors at the endpoints of the edge over
between the vectors at the endpoints of the edge over  . Comparing this probability to
. Comparing this probability to  , in expectation the ratio is always at least 0.87856.) Assuming the Unique Games Conjecture, it can be shown that this approximation ratio is essentially optimal.
, in expectation the ratio is always at least 0.87856.) Assuming the Unique Games Conjecture, it can be shown that this approximation ratio is essentially optimal.Since the original paper of Goemans and Williamson, SDPs have been applied to develop numerous approximation algorithms. Recently, Prasad Raghavendra has developed a general framework for constraint satisfaction problems based on the Unique Games Conjecture.[1]
Algorithms
There are several types of algorithms for solving SDPs. These algorithms output the value of the SDP up to an additive error in time that is polynomial in the program description size and
in time that is polynomial in the program description size and  .
.Interior point methods
Most codes are based on interior point methods (CSDP, SeDuMi, SDPT3, DSDP, SDPA). Robust and efficient for general linear SDP problems. Restricted by the fact that the algorithms are second-order methods and need to store and factorize a large (and often dense) matrix.Bundle method
The code ConicBundle formulates the SDP problem as a nonsmooth optimization problem and solves it by the Spectral Bundle method of nonsmooth optimization. This approach is very efficient for a special class of linear SDP problems.Other
Algorithms based on augmented Lagrangian method (PENSDP) are similar in behavior to the interior point methods and can be specialized to some very large scale problems. Other algorithms use low-rank information and reformulation of the SDP as a nonlinear programming problem (SPDLR).Software
The following codes are available for SDP:SDPA, CSDP, SDPT3, SeDuMi, DSDP, PENSDP, SDPLR, ConicBundle
SeDuMi runs on MATLAB and uses the Self-Dual method for solving general convex optimization problems.
![\begin{array}{rl}
{\displaystyle \min_{x^1, \ldots, x^n \in \mathbb{R}^n}} & {\displaystyle \sum_{i,j \in [n]} c_{i,j} (x^i \cdot x^j)} \\
\text{subject to} & {\displaystyle \sum_{i,j \in [n]} a_{i,j,k} (x^i \cdot x^j) \leq b_k \qquad \forall k}. \\
\end{array}](http://upload.wikimedia.org/wikipedia/en/math/f/8/8/f88255c018dce0154f44961e90618d9b.png)




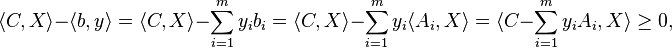

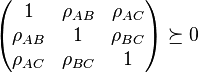


No comments:
Post a Comment